A fast, reliable, and open-source convex cone solver.

SCS (Splitting Conic Solver) is a numerical optimization package for solving large-scale convex quadratic cone problems. The code is freely available on GitHub. It solves primal-dual problems of the form

\[\begin{split}\begin{array}{lcr} \begin{array}{ll} \mbox{minimize} & (1/2)x^\top P x + c^\top x\\ \mbox{subject to} & Ax + s = b\\ & s \in \mathcal{K} \end{array} &\quad& \begin{array}{ll} \mbox{maximize} & -(1/2)x^\top P x - b^\top y\\ \mbox{subject to} & Px + A^\top y + c = 0\\ & y \in \mathcal{K}^* \end{array} \end{array}\end{split}\]

over variables

\(x \in \mathbf{R}^n\)	primal variable
\(y \in \mathbf{R}^m\)	dual variable
\(s \in \mathbf{R}^m\)	slack variable

with data

\(A \in \mathbf{R}^{m \times n}\)	sparse data matrix, see Data matrices
\(P \in \mathbf{S}_+^{n}\)	sparse, symmetric positive semidefinite matrix
\(c \in \mathbf{R}^n\)	dense primal cost vector
\(b \in \mathbf{R}^m\)	dense dual cost vector
\(\mathcal{K} \subseteq \mathbf{R}^m\)	nonempty, closed, convex cone, see Cones
\(\mathcal{K}^* \subseteq \mathbf{R}^m\)	dual cone to \(\mathcal{K}\)

At termination SCS will either return points \((x^\star,y^\star,s^\star)\) that satisfies the optimality conditions to the desired accuracy, or a certificate of primal or dual infeasibility to the designated infeasibility accuracy.

Features

• Efficient: Designed to scale to large problems.

• Flexible: Supports quadratic objectives and a large range of cones.

• Free and open source: Distributed under the permissive MIT license.

• Detects infeasibility: Robustly and reliably detects infeasible problems.

• Interfaces: Bindings for many languages, including C, Python, Julia, R, MATLAB, and Ruby.

• Warm starts: Easily warm-started, and the matrix factorization can be cached.

• Matrix-free: Optionally use an indirect linear system solver, or a GPU version.

• Supported: A supported solver in CVX, CVXPY, YALMIP, Convex.jl and JuMP.

• Accelerated: Includes acceleration that can improve convergence to high accuracy.

• Battle-tested: The first ADMM-based solver available, and in wide usage.

Performance

SCS is a fast and reliable optimization library. For instance, it is one of the most performant solvers as determined by the third-party QP solvers benchmark on the challenging Maros-Meszaros QP test suite. This is despite SCS being a general quadratic conic solver and not specifically tailored for QPs.

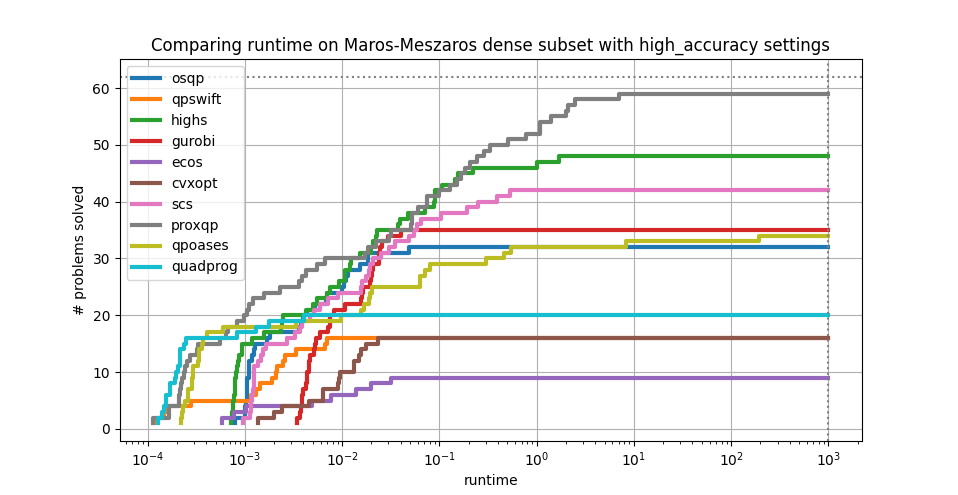
SCS is faster and more reliable than most other solvers.

Development

SCS is a community project, built from the contributions of many researchers and engineers. The primary maintainer is Brendan O’Donoghue. We appreciate all contributions. To get involved, see our contributing guide.